Generally, there are two types of logarithmic equations. Study each case carefully before you start looking at the worked examples below.
- The first type looks like this.

If you have a single logarithm on each side of the equation having the same base, you can set the arguments equal to each other and then solve. The arguments here are the algebraic expressions represented by [latex]\color{blue}M[/latex] and [latex]\color{red}N[/latex].
- Thesecond typelooks like this.

If you have a single logarithm on one side of the equation, you can express it as an exponential equation and solve it.
Let’s learn how to solve logarithmic equations by going over someexamples.
Examples of How to Solve Logarithmic Equations
Example 1: Solve the logarithmic equation.

Since we want to transform the left side into a single logarithmic equation, we should use the Product Rule in reverse to condense it. Here is the rule, just in case you forgot.

- Given

- Apply Product Rule from Log Rules.

- Distribute: [latex]\left( {x + 2} \right)\left( 3 \right) = 3x + 6[/latex]

- Drop the logs, set the arguments (stuff inside the parenthesis) equal to each other.

- Then solve the linear equation. I know you got this part down!

Just a big caution. ALWAYS check your solved values with the original logarithmic equation.
Remember:
- It is OKAY for [latex]x[/latex] to be [latex]0[/latex] or negative.
- However, it is NOT ALLOWED to have a logarithm of a negative number or a logarithm of zero, [latex]0[/latex], when substituted or evaluated into the original logarithm equation.
CAUTION: The logarithm of a negative number, and the logarithm of zero are both not defined.
[latex]{\log _b}\left( {{\rm{negative\,\,number}}} \right) = {\rm{undefined}}[/latex]
[latex]{\log _b}\left( 0 \right) = {\rm{undefined}}[/latex]
Let’s check our answer to see if [latex]x=7[/latex] is a valid solution. Substitute it back into the original logarithmic equation and verify if it yields a true statement.

Yes! Since [latex]x = 7[/latex] checks, we have a solution at [latex]\color{blue}x = 7[/latex].
Example 2: Solve the logarithmic equation.

Start by condensing the log expressions on the left into a single logarithm using the Product Rule. We want to have a single log expression on each side of the equation. Be ready though to solve for a quadratic equation since [latex]x[/latex] will have a power of [latex]2[/latex].
- Given

- Apply Product Rule from Log Rules

- Simplify: [latex]\left( x \right)\left( {x – 2} \right) = {x^2} – 2x[/latex]

- Drop the logs, set the arguments (stuff inside the parenthesis) equal to each other

- Solve the quadratic equation using the factoring method. But you need to move everything on one side while forcing the opposite side equal to [latex]0[/latex].

- Set each factor equal to zero, then solve for [latex]x[/latex].
[latex]x – 5 = 0[/latex] implies that [latex]x = 5[/latex]
[latex]x + 2 = 0[/latex] implies that [latex]x = – 2[/latex]
So the possible solutions are[latex]x = 5[/latex] and[latex]x = – 2[/latex]. Remember to always substitute the possible solutions back to the original log equation.
Let’s check our potential answers [latex]x = 5[/latex] and [latex]x = – 2[/latex] if they will be valid solutions.
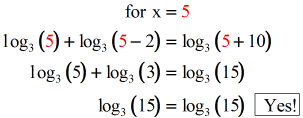

After checking our values of [latex]x[/latex], we found that [latex]x = 5[/latex] is definitely a solution. However, [latex]x =-2[/latex] generates negative numbers inside the parenthesis ( log of zero and negative numbers are undefined) which makes us eliminate [latex]x =-2[/latex] as part of our solution.
Therefore, the final solution is just [latex]\color{blue}x=5[/latex]. We disregard [latex]x=-2[/latex] because it is an extraneous solution.
Example 3: Solve the logarithmic equation.

This is an interesting problem. What we have here are differences of logarithmic expressions on both sides of the equation. Simplify or condense the logs on both sides by using the Quotient Rule.

- Given

- The difference of logs is telling us to use the Quotient Rule. Convert the subtraction operation outside into a division operation inside the parenthesis. Do it to both sides of the equations.

- I think we are ready to set each argument equal to each other since we can reduce the problem to have a single log expression on each side of the equation.

- Drop the logs, and set the arguments (stuff inside the parenthesis) equal to each other. Note that this is a Rational Equation. One way to solve it is to get its Cross Product.

- It looks like this after getting its Cross Product.

- Simplify both sides by the Distributive Property. At this point, we realize that it is just a Quadratic Equation. No big deal then. Move everything to one side, which forces one side of the equation to be equal to zero.

- This is easily factorable. Now set each factor to zero and solve for [latex]x[/latex].

- So, these are our possible answers.

I will leave it to you to check our potential answers back into the original log equation. You should verify that [latex]\color{blue}x=8[/latex] is the only solution, while [latex]x =-3[/latex] is not since it generates a scenario wherein we are trying to get the logarithm of a negative number. Not good!
Example 4: Solve the logarithmic equation.

If you see “log” without an explicit or written base, it is assumed to have a base of [latex]10[/latex]. In fact, a logarithm with base [latex]10[/latex] is known as the common logarithm.
What we need is to condense or compress both sides of the equation into a single log expression. On the left side, we see a difference of logs which means we apply the Quotient Rule while the right side requires the Product Rule because they’re the sum of logs.
There’s just one thing that you have to pay attention to on the left side. Do you see that coefficient [latex]\Large{1 \over 2}\,[/latex]?
Well, we have to bring it up as an exponent using the Power Rule in reverse.

- Given

- Bring up that coefficient [latex]\large{1 \over 2}[/latex] as an exponent (refer to the leftmost term)

- Simplify the exponent (still referring to the leftmost term)

- Then, condense the logs on both sides of the equation.Use the Quotient Rule on the left and Product Rule on the right.

- Here, I used different colors to show that since we have the same base (if not explicitly shown it is assumed to be base [latex]10[/latex]), it’s okay to set them equal to each other.

- Dropping the logs and just equating the arguments inside the parenthesis.

- At this point, you may solve the Rational Equation by performing Cross Product.Move all the terms on one side of the equation, then factor them out.

- Set each factor equal to zero and solve for [latex]x[/latex].

It’s time to check your potential answers. When you check [latex]x=0[/latex] back into the original logarithmic equation, you’ll end up having an expression that involves getting the logarithm of zero, which is undefined, meaning – not good! So, we should disregard or drop [latex]\color{red}x=0[/latex] as a solution.
Checking [latex]\Large{x = {3 \over 4}}[/latex], confirms that indeed [latex]\Large{\color{blue}{x = {3 \over 4}}}[/latex] is the only solution.
Example 5: Solve the logarithmic equation.

This problem involves the use of the symbol [latex]\ln[/latex] instead of [latex]\log[/latex] to mean logarithm.
Think of [latex]\ln[/latex] as a special kind of logarithm using base [latex]e[/latex] where [latex]e \approx 2.71828[/latex].

- Given
- Use Product Rule on the right side

- Write the variable first, then the constant to be ready for the FOIL method.

- Simplify the two binomials by multiplying them together.

- At this point, I simply color-coded the expression inside the parenthesis to imply that we are ready to set them equal to each other.

- Yep! This is where we say that the stuff inside the left parenthesis equals the stuff inside the right parenthesis.

- Solve the Quadratic Equation using the Square Root Method. You do it by isolating the squared variable on one side and the constant on the other. Then we apply the square root on both sides.
Don’t forget the [latex]\pm[/latex]symbol.

- Simplifying further, we should get these possible answers.

Check if the potential answers found above are possible answers by substituting them back to the original logarithmic equations.
You should be convinced that the ONLY valid solution is [latex]\large{\color{blue}x = {1 \over 2}}[/latex] which makes [latex]\large{\color{red}x = -{1 \over 2}}[/latex] an extraneous answer.
Example 6: Solve the logarithmic equation.

There is only one logarithmic expression in this equation. We consider this as the second case wherein we have

We will transform the equation from the logarithmic form to the exponential form, then solve it.
- Given

- I color-coded the parts of the logarithmic equation to show where they go when converted into exponential form.

- The blue expression stays at its current location, but the red number becomes the exponent of the base of the logarithm which is [latex]3[/latex].

- Simplify the right side, [latex]{3^4} = 81[/latex].

- Finish off by solving the two-step linear equation that arises.

You should verify that the value [latex]\color{blue}x=12[/latex] is indeed the solution to the logarithmic equation.
Example 7: Solve the logarithmic equation.

Collect all the logarithmic expressions on one side of the equation (keep it on the left) and move the constant to the right side. Use the Quotient Rule to express the difference of logs as fractions inside the parenthesis of the logarithm.
- Given

- Move all the logarithmic expressions to the left of the equation, and the constant to the right.

- Use the Quotient Rule to condense the log expressions on the left side.

- Get ready to write the logarithmic equation into its exponential form.

- The blue expression stays in its current location, but the red constant turns out to be the exponent of the base of the log.

- Simplify the right side of the equation since [latex]5^{\color{red}1}=5[/latex].

- This is a Rational Equation due to the presence of variables in the numerator and denominator.
I would solve this equation using the Cross Product Rule. But I have to express first the right side of the equation with the explicit denominator of [latex]1[/latex]. That is, [latex]5 = {\large{{5 \over 1}}}[/latex]

- Perform the Cross-Multiplication and then solve the resulting linear equation.

When you check [latex]x=1[/latex] back to the original equation, you should agree that [latex]\large{\color{blue}x=1}[/latex] is the solution to the log equation.
Example 8: Solve the logarithmic equation.

This problem is very similar to #7. Let’s gather all the logarithmic expressions to the left while keeping the constant on the right side. Since we have the difference of logs, we will utilize the Quotient Rule.
- Given

- Move the log expressions to the left side, and keep the constant to the right.

- Apply the Quotient Rule since they are the difference of logs.

- I used different colors here to show where they go after rewriting in exponential form.

- Notice that the expression inside the parenthesis stays in its current location, while the [latex]\color{red}5[/latex] becomes the exponent of the base.

- To solve this Rational Equation, apply the Cross Product Rule.

- Simplify the right side by the distributive property.It looks like we are dealing with a quadratic equation.

- Move everything to the left side and make the right side just zero.
Factor out the trinomial. Set each factor equal to zero then solve for [latex]x[/latex].

- When you solve for [latex]x[/latex], you should get these values of [latex]x[/latex] as potential solutions.

Make sure that you check the potential answers from the original logarithmic equation.
You should agree that [latex]\color{blue}x=-32[/latex] is the only solution. That makes [latex]\color{red}x=4[/latex] an extraneous solution, so disregard it.
Example 9: Solve the logarithmic equation

I hope you’re getting the main idea now on how to approach this type of problem. Here we see three log expressions and a constant. Let’s separate the log expressions and the constant on opposite sides of the equation.
- Let’s keep the log expressions on the left side while the constant on the right side.

- Start by condensing the log expressions using the Product Rule to deal with the sum of logs.

- Then further condense the log expressions using the Quotient Rule to deal with the difference of logs.

- At this point, I used different colors to illustrate that I’m ready to express the log equation into its exponential equation form.

- Keep the expression inside the grouping symbol (blue) in the same location while making the constant [latex]\color{red}1[/latex] on the right side as the exponent of the base [latex]7[/latex].

- Solve this Rational Equation using Cross Product. Express [latex]7[/latex] as [latex]\large{7 \over 1}[/latex].

- Cross multiply.

- Move all terms to the left side of the equation. Factor out the trinomial. Next, set each factor equal to zero and solve for [latex]x[/latex].

- These are your potential answers. Always check your values.

It’s obvious that when we plug in [latex]x=-8[/latex] back into the original equation, it results in a logarithm with a negative number. Therefore, you exclude [latex]\color{red}x=-8[/latex] as part of your solution.
Thus, the only solution is [latex]\color{blue}x=11[/latex].
Example 10: Solve the logarithmic equation.

- Keep the log expression on the left, and move all the constants on the right side.

- Simplify.

- I think we’re ready to transform this log equation into the exponential equation.

- The expression inside the parenthesis stays in its current location while the constant [latex]3[/latex] becomes the exponent of the log base [latex]3[/latex].

- Simplify the right side since [latex]{3^3}=27[/latex].What we have here is a simple Radical Equation.
Check this separate lesson if you need a refresher on how to solve different types of Radical Equations.

- To get rid of the radical symbol on the left side, square both sides of the equation.

- After squaring both sides, it looks like we have a linear equation. Just solve it as usual.

Check your potential answer back into the original equation.
After doing so, you should be convinced that indeed [latex]\color{blue}x=-104[/latex] is avalid solution.
You may also be interested in these related math lessons or tutorials:
Condensing Logarithms
Expanding Logarithms
Logarithm Explained
Logarithm Rules
